MCUV - Movimiento Circular Uniformemente Variado

Ahora que ya conoces el Movimiento Circular Uniformemente Variado (MCUV) y sus variables, vamos a repasar sus principales fórmulas.


ECUACIONES ANGULARES
Cuando te refieres a los cambios de arco en el movimiento y estás utilizando los radianes como unidad de medida, debes utilizar las ecuaciones angulares.
Recuerda que un movimiento circular es considerado como uniformemente variado, cuando su aceleración angular es constante, es decir:


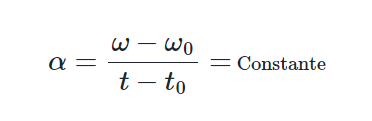
De esta relación, despejamos la velocidad angular, de la siguiente manera:


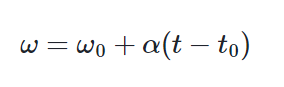
Si deseamos saber la posición de un móvil en un tiempo dado, podemos utilizar:


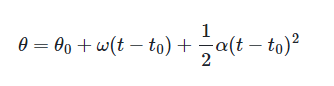
Estas dos fórmulas pueden simplificarse cuando el tiempo inicial es cero, de tal manera que tenemos:


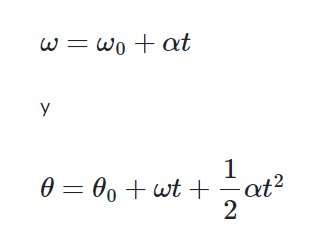
Si deseas saber la velocidad angular de un móvil que se mueve con MCUV, teniendo como datos su posición y su aceleración angular, puedes utilizar:


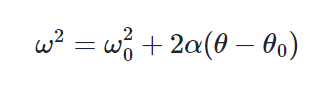
Igualmente, podemos relacionar el desplazamiento, o la variación de posición angular, como:


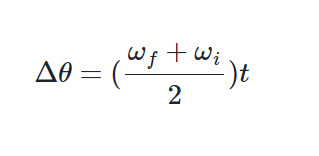
ECUACIONES TAGENCIALES
Son aquellas propias del movimiento circular uniformemente variado y se refieren a lo que ocurre en un punto durante el movimiento circular. Cuando tienes datos de velocidad en m/s, debes utilizar las ecuaciones tangenciales.

RELACIONANDO VARIABLES TANGENCIALES Y ANGULARES
La velocidad tangencial, es decir, la velocidad que experimenta un móvil en un determinado punto de la circunferencia, puede expresarse en relación a la velocidad angular, de la siguiente manera:


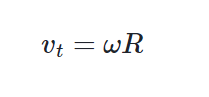
ACELERACIONES
En un movimiento circular se presenta una aceleración en dirección tangencial a la circunferencia conocida como aceleración tangencial y otra aceleración en dirección radial y dirigida hacia el centro de la trayectoria, llamada aceleración centrípeta.
Como la velocidad es una magnitud vectorial, la aceleración tangencial se produce por un cambio en el módulo de la velocidad tangencial, mientras que la aceleración centrípeta se produce por el cambio en la dirección y sentido del vector velocidad.
Por tanto, un móvil con MCUV posee, además de aceleración centrípeta, una aceleración tangencial. Se produce entonces una aceleración resultante, que como su nombre lo indica, es la resultante de ambas aceleraciones.
Gráficamente, tenemos:


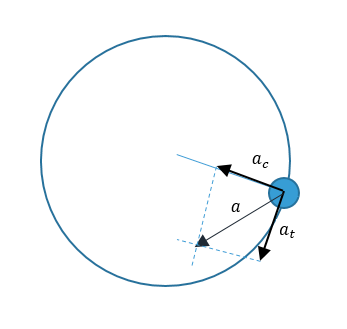
De esto, podemos concluir que:


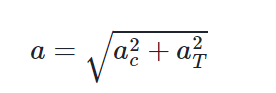
La aceleración centrípeta es función de la velocidad tangencial, así como de la velocidad angular, por lo que puede hallarse de dos maneras, según los datos que tengas:


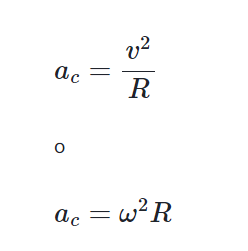
Mientras que la aceleración tangencial va a depender de la aceleración angular de la siguiente manera:


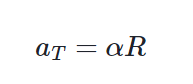
¡PARA MAS INFORMACIÓN SOBRE MCUV HAZ CLICK AQUI!